Kinetik und Geometrie

Einige Prinzipien der Mechanik
am Bildschirm blättern oder als PDF download …

Cubus – das ABC des Würfels
am Bildschirm blättern oder als PDF download …

Minimal Konstruktionen – 17 Beispiele
am Bildschirm blättern oder als PDF download

Die Platonischen Körper (nach dem griechischen Philosophen Platon) sind die Polyeder mit größtmöglicher Symmetrie. Jeder von ihnen wird von mehreren deckungsgleichen (kongruenten) ebenen regelmäßigen Vielecken begrenzt. Eine andere Bezeichnung ist reguläre Körper (von lat. corpora regularia[1][2]).

Es gibt fünf platonische Körper. Ihre Namen enthalten die griechisch ausgedrückte Zahl ihrer begrenzenden Flächen und eder als Abwandlung des griechischen Wortes ἕδρα (hedra) (s. auch Polyeder), deutsch (Sitz-)Fläche.

Tetraeder
(Vierflächner, Oberfläche aus vier Dreiecken)

Hexaeder
(Sechsflächner, Oberfläche aus sechs Quadraten) – der Würfel

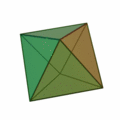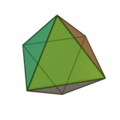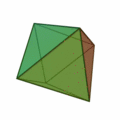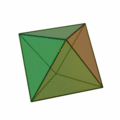
Oktaeder
(Achtflächner, Oberfläche aus acht Dreiecken)

Dodekaeder
(Zwölfflächner, Oberfläche aus zwölf Fünfecken) – auch Pentagondodekaeder genannt, um auf die Oberfläche aus Fünfecken als seine Besonderheit hinzuweisen

Ikosaeder
(Zwanzigflächner, Oberfläche aus zwanzig Dreiecken)

Die Platonischen Körper sind konvex. In jeder Ecke des Körpers treffen jeweils gleich viele gleich lange Kanten zusammen, an jeder Kante treffen sich zwei deckungsgleiche Flächen, und jede Fläche hat gleich viele Ecken. Es ist also nicht möglich, irgendwelche zwei Körperecken, Kanten und Flächen aufgrund von Beziehungen zu anderen Punkten des Polyeders voneinander zu unterscheiden.

Alternativ lassen sich die platonischen Körper definieren als diejenigen Polyeder, für die es zu einem beliebigen Paar von Seitenflächen, Kanten oder Ecken immer eine Symmetrieabbildung gibt, die diese Flächen, Kanten oder Ecken vertauscht. Dies ist gemeint mit der größtmöglichen Symmetrie.

Quelle: Wikipedia